LA ELIPSE

                                                          LA        ELIPSE

La elipse es una línea curva, cerrada y plana cuya definición más usual es:

La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.

Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.¹ Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Elementos gráficos de la elipse

Nomenclatura

La descripción corresponde a las imágenes de la derecha.

Los diámetros principales o ejes principales son los diámetros máximo y mínimo de la elipse, perpendiculares entre sí y que pasan por el centro. Tradicionalmente son nombrados A-B el mayor y B-C el menor, aunque también se utilizan otras nomenclaturas, como A-A' el mayor y B-B' el menor.

El centro de la elipse se suele nombrar O (origen). En la circunferencia los focos coinciden con el centro.

Los focos se suelen nombrar con la letra F acompañada de algún medio de diferenciarlos, F₁ - F₂, o F' - F" .

El diámetro mayor de la elipse se suele designar 2a, siendo a el semieje mayor. El semieje menor se denomina b y el diámetro menor 2b. La distancia de cada foco al centro se denomina c.

Los segmentos que van de cada foco a un punto de la elipse se denominan radios vectores; la suma de los radios vectores de cada punto es una constante igual a 2a.

Ecuaciones de la elipse

En coordenadas cartesianas

Forma cartesiana centrada en el origen

La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:

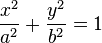
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisasy b al eje de las ordenadas la elipse

es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2εa, siendo ε la excentricidady a el semieje mayor.

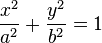
Forma cartesiana centrada fuera del origen

Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:

PARA SU MEJOR ENTENDIMIENTO DALE CLICK POR FAVOR.
http://www.vitutor.com/geo/coni/g_3.html

RECOMIENDO POR SU CONTENIDO Y POR SU EXPLICACION SENCILLA, FACIL DE ENTENDER. ADEMAS DE APORTAR EJERCICIOS PARA NUESTRA PRACTICA.

LA PARABOLA

LA PARABOLA

LOS ELEMENTOS BASICOS DE UNA PARABOLA SON:

VERTICE.    En el origen o fuera del origen.  V (0,0)   o   V( h,k)

FOCO.        Siempre se encuentra localizado dentro de la Parábola. (p)

LADO RECTO.         L.R.= / 4p /

DIRECTRIZ.        x = p      o     x= - p

Para trazar una parábola es necesario conocer las coordenadas de su foco y de su vértice para determinar su posición, eje de simetría o dirección en que abre.

CUANDO LA PARABOLA PRESENTA SU VERTICE EN EL ORIGEN, SU ECUACIÓN SERÁ:

CUANDO LA PARABOLA PRESENTA SU VERTICE  FUERA DEL ORIGEN, SU ECUACIÓN SERÁ:

 

CUANDO SU EJE COINCIDE CON EL EJE DE LAS  Y.

LOS ELEMENTOS SE DETERMINAN POR:

VERTICE:   ( h, k )

FOCO:      ( h,  k+p )

DIRECTRIZ:    y = k - p

Si la parábola abre hacia abajo, el valor de p sera negativo.

CUANDO EL EJE DE  LA PARABOLA COINCIDE CON EL EJE  X SU ECUACIÓN SERA:

DONDE:

VERTICE:   ( h, k )

FOCO:  (h + p ,   k)

DIRECTRIZ:  x = h - p

PARA ENCONTRAR LA ECUACION GENERAL DE LA PARABOLA SE SIGUE EL PROCESO TAL COMO LO HICIMOS  PARA LA CIRCUNFERENCIA.  SOLO DEBEMOS DESARROLLAR BINOMIOS.

RECUERDEN ESTA PAGINA.  YA LA HABIAMOS RECOMENDADO.   VISITENLA Y VERAN QUE TRAE MUY BUENA INFORMACIÓN.  

PARA LO QUE NOS INTERESA AL MOMENTO. VISITEN EL ICONO GEOMETRIA ANALITICA.   

http://math2me.com/

MODULO 3

LAS     CÓNICAS

Para el presente módulo trabajaremos las figuras cónicas que son aquellas que resultan al realizar diferentes cortes a un cono.

El módulo lo trabajaremos en función a las cuatro figuras resultantes que son:

LA CIRCUNFERENCIA.

LA ELIPSE

LA PARÁBOLA  Y

LA HIPÉRBOLA

INICIAMOS CON LA CIRCUNFERENCIA

I.   LA CIRCUNFERENCIA.

      Ecuación de la circunferencia con  centro en el origen  C(0,0) y radio   r.

       

RECUERDA: PARA EL TRAZADO DE LA CIRCUNFERENCIA SOLO NECESITAMOS LOS DATOS DEL CENTRO Y DE SU RADIO PARA SUSTITUIR EN LA FORMULA CANÓNICA. 

Ecuación con centro fuera del origen:  C( h, k) y radio  r.    

Ecuación General de la Circunferencia.

http://www.youtube.com/watch?v=HGYMfv7OW1A}

http://www.youtube.com/watch?v=pjVGASYPKMg

ESTA INTERESANTE, RECOMIENDO.

RECTAS Y PUNTOS NOTABLES DE UN TRIANGULO

HEMOS APRENDIDO EN LOS TEMAS ANTERIORES DE LA IMPORTANCIA DE CONOCER PUNTOS MEDIOS DE UN SEGMENTO; PENDIENTE Y ÁNGULO DE INCLINACIÓN DE UNA RECTA; ÁNGULO DE INTERSECCIÓN ENTRE DOS RECTAS, PERO SOBRE TODO, HEMOS ANALIZADO Y DETERMINADO LAS DISTINTAS FORMAS DE REPRESNTAR LA ECUACIÓN DE UNA RECTA.

EN ESTA OCASIÓN NOS DETENDREMOS A UTILIZAR TODAS ESTAS HERRAMIENTAS EN EL TEMA DE RECTAS Y PUNTOS NOTABLES DE UN TRIÁNGULO DONDE:  PRIMERAMENTE  DEBEREMOS ENTENDER CADA UNO DE LOS CONCEPTOS.

• MEDIANA- GRAVICENTRO O BARICENTRO

ES EL SEGMENTO TRAZADO DESDE UN VÉRTICE DEL TRIÁNGULO HACIA EL PUNTO MEDIO DEL LADO OPUESTO DEL MISMO.   EL PUNTO DE CONCURRENCIA O DE INTERSECCIÓN ENTRE LAS MEDIANAS SE LE NCONOCE COMO GRAVICENTRO O BARICENTRO.
















OJO:  Para encontrar la ecuación de cada una de las mediatrices solo necesitamo
Conocer los puntos medios de cada uno de los lados del triángulo. Luego con este punto y los puntos de los vértices del triángulo, aplicamos la ecuación de dos puntos la sustituímos y ya está.

• MEDIATRICES- CIRCUNCENTRO.

La mediatriz de un segmento es la perpendicular que pasa por el punto medio, es decir, es el lugar geométrico de los puntos que esquidistan de los extremos del segmento.  El punto de concurrencia o de in tersección de las mediatrices se llama   CIRCUNCENTRO




OJO:   Para encontrar la ecuación de cada una de las mediatrices necesitamos:
El punto medio de cada uno de los lados del triángulo; la pendiente de cada uno de los lados; luego con la definición de perpendicularidad  que nos dice: para que dos rectas sean perpendiculares, sus pendientes deberán ser recíprocas y de signo contrario o que el producto de ambas sea( -1 ). Vamos a conocer básicamente los elementos necesarios para encontrar su ecuación; un punto(punto medio) y la pendiente. Aplicamos la ecuación punto-pendiente, la sustituímos y listo.

• ALTURAS DE UN TRIANGULO- ORTOCENTRO.

Ls alturs del triángulo es el segmento de recta que se traza desde un vértice perpendicularmente a su lado opuesto. Al punto de intersección de las alturas del triangulo se le llama ORTOCENTRO.

                          

OJO:  Para encontrar las alturas del triángulo necesitamos:

Las pendientes de cada uno de los lados del triángulo, luego aplicamos el concepto de perpendicularidad como en el caso de las mediatrices. Con el dato de la pendiente y conociendo cada uno de los vértices del triángulo,  tendremos de igual manera un punto y la pendiente por lo que podremos encontrar la ecuación sustituyendo directamente en la ecuación de punto- pendiente.

• BISECTRIZ-INCENTRO.

La bisectriz de un ángulo es la semirrecta interior del ángulo, que lo divide en dos partes o ángulos iguales, es decir, es el lugar geométrico de los puntos equidistantes de los lados del ángulo.  Al punto de concurrencia de las bisectrices se le llama INCENTRO.

  



OJO:  Para encontrar las ecuaciones de cada una de las bisectrices necesitamos saber el teorema o fórmula que nos ayude a encontrar la distancia de un punto a una recta, las ecuaciones de cada uno de los lados del triángulo y aplicando el criterio de que el Incentro  guarda una misma distancia hacia las rectas que considera la bisectriz, igualamos la ecuación de las distancias d1= d2, se desarrolla algebraicamente y listo.


Propongo ver:
http://www.youtube.com/watch?v=VMK9B4MacEc


sencillisimo con geogebra.

ECUACION DE LA RECTA

LA LINEA RECTA

GEOMÉTRICAMENTE: Una  línea recta se define como la distancia más corta entre dos puntos.
ANALÍTICAMENTE:  Una línea recta se define como una ecuación de primer gradao con dos variables.
GRÁFICAMENTE: Se define como el  lugar geométrico de la sucesión de puntos, tales que, tomados dos puntos diferentes cualesquiera P1 (x1,y1) y  P2 (x2, y2) del lugar geométrico, el valor de la pendiente  m es siempre constante.
Analíticamente, se conocen diversas formas de representación de la ecuación de una recta:

TEOREMA:
La ecuación de la recta que pasa por el punto P1(x1, y1) y tiene la pendiente dada  m, es :
y - y1 = m ( x - x1)

TEOREMA:
La ecuación de la recta cuya pendiente es m  y tiene su ordenada en el origen (b), es :
y = mx + b

A esta ecuación se le conoce con el nombre de ecuación ordenada en el origen  o ecuación forma común

TEOREMA:
La ecuación de la recta que intersecta los ejes coordenados x y y en los puntos (a , 0 ) y (0 , b) , respectivamente, es:

x/a  + y/b = 1
donde a es la intersección con el eje coordenado  x
donde b es la intersección con el eje coordenado y 
A esta recta tanbién se le conoce con el nombre de Simétrica o Canónica

TEOREMA:

La ecuacion lineal en las variables x y y, denotada por Ax + By +C = 0, representa una recta  y reciprocamente.

Donde :  a = -C/A  ;  b = - C/B  ;  m = -A/B

A esta ecuacion se le conoce como la ecuacion general de una recta.

Recomiendo, por favor veanlos y practiquen

http://www.youtube.com/watch?v=W3wRESJsc9Q

http://www.youtube.com/watch?v=bfZ57ESvFok

PLANANEACION SEGUNDO MODULO GEOMETRIA ANALITICA

PLANEACION CURRICULAR PARA LA SEGUNDA UNIDAD.

TEMA  :  LA LINEA RECTA.

• PROPIEDADES
• PENDIENTE Y ANGULO DE INCLINACION DE UNA RECTA
• FORMAS DE ECUACION DE UNA RECTA Y TRANSFORMACIONES
• INTERSECCION DE RECTAS Y ANGULO DE INTERSECCION ENTRE DOS RECTAS
• RECTAS NOTABLES DE UN TRIANGULO.

ÁREA DE POLÍGONOS EN FUNCIÓN DE SUS VÉRTICES

   ÁREA DE POLÍGONOS EN FUNCIÓN DE LAS COORDENADAS DE SUS VÉRTICES.

CUANDO TENEMOS  UN  POLÍGONO CUALESQUIERA  EN UN  PLANO CARTESIANO Y QUEREMOS ENCONTRAR EL ÁREA TOTAL, EN OCASIONES SE NOS HACE MUY COMPLICADO POR LA FIGURA DE QUE SE TRATE, COMO EN EL EJEMPLO ANTERIOR, ES NECESARIO DIVIDIR EL  POLÍGONO EN ÁREAS DIVERSAS Y SENCILLAS DE CALCULAR PARA LUEGO SUMARLAS Y CONOCER ASÍ EL ÁREA TOTAL DEL POLÍGONO.

ES MEJOR LOCALIZAR LAS COORDENADAS DE LOS VÉRTICES, COLOCAR ESTAS COORDENADAS EN UNA DETERMINANTE SIGUIENDO SIEMPRE UN ORDEN               ( SENTIDO CONTRARIO AL MOVIMIENTO DE LAS MANECILLAS DEL RELOJ), INICIANDO DE CUALQUIERA DE SUS VÉRTICES.  SE RESUELVE LA DETERMINANTE Y LISTO.
DEBEMOS RECORDAR, QUE EN LA DETERMINANTE SE COLOCAN TODOS Y CADA UNO DE LOS VÉRTICES DE ACUERDO AL POLÍGONO QUE SE QUIERA RESOLVER, COLOCANDO SIEMPRE AL FINAL LA  COORDENADA CON QUE SE INICIÓ. SENCILLÍSIMO.   SI LA FIGURA ES UN TRIÁNGULO, SE COLOCAN CUATRO RENGLONES; SI ES CUADRADO, SE COLOCAN CINCO RENGLONES; SI ES UN  PENTÁGONO SERÁN SEIS RENGLONES Y ASÍ SUCESIVAMENTE.


RECOMIENDO Y OJALÁ SEA DE GRAN UTILIDAD.


http://www.youtube.com/watch?v=8vg_SwjLW5U
SUERTE.